목차
Heap 힙
우선순위 큐
우선순위를 가진 원소를 삽입할 수 있고, 우선순위가 가장 큰 원소를 빼내줄 수 있는 자료구조
힙
대표적인 우선순위 큐, 완전 이진 트리(Complete Binary Tree) 구조 사용
포화 이진 트리(Full Binary Tree): 루트부터 시작해 모든 노드가 정확히 자식 노드를 2개씩 가지면서 꽉 채워진 트리, 노드의 총 수는 2k-1개
완전 이진 트리(Complete Binary Tree)

힙의 조건
- 완전 이진 트리
- 힙 특성: 모든 노드는 값을 갖고, 자식 노드(들) 값보다 크거나 같다. (최대 힙)
힙 배열
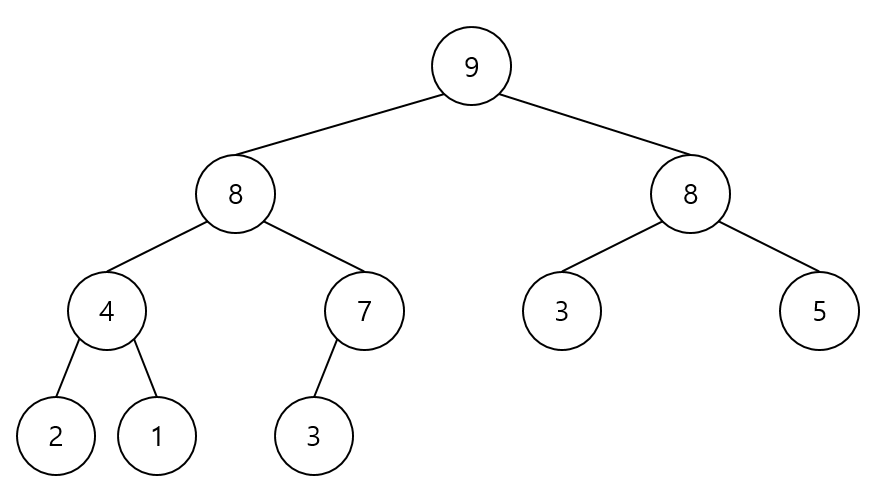
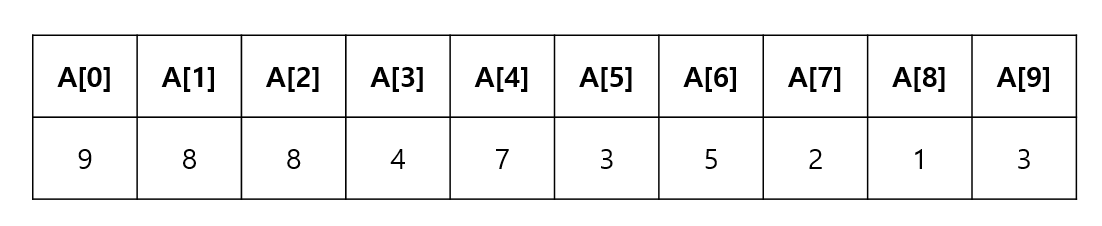
루트 노드부터 순서대로 배열에 담아 관리
삽입
A[8]에 원소 8 삽입
- 배열의 맨 끝에 8을 삽입
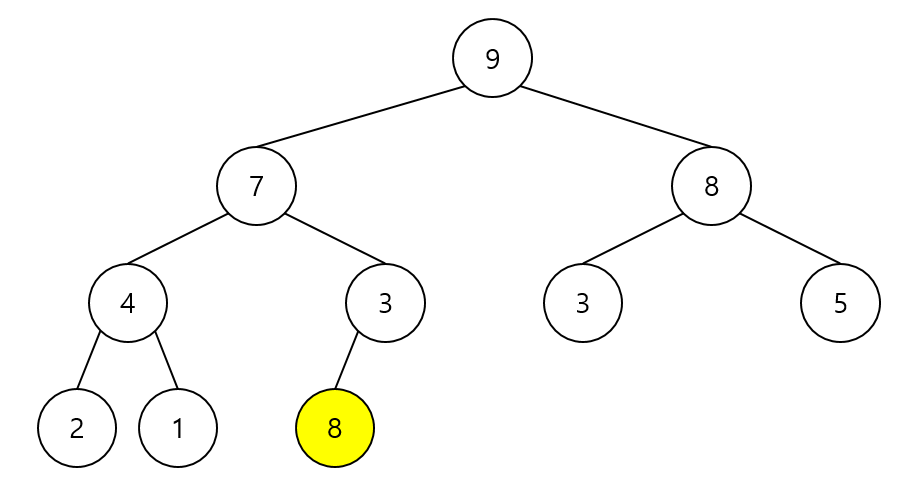
- 8을 자신의 부모 3과 비교 → 8이 더 크므로 자리 교환
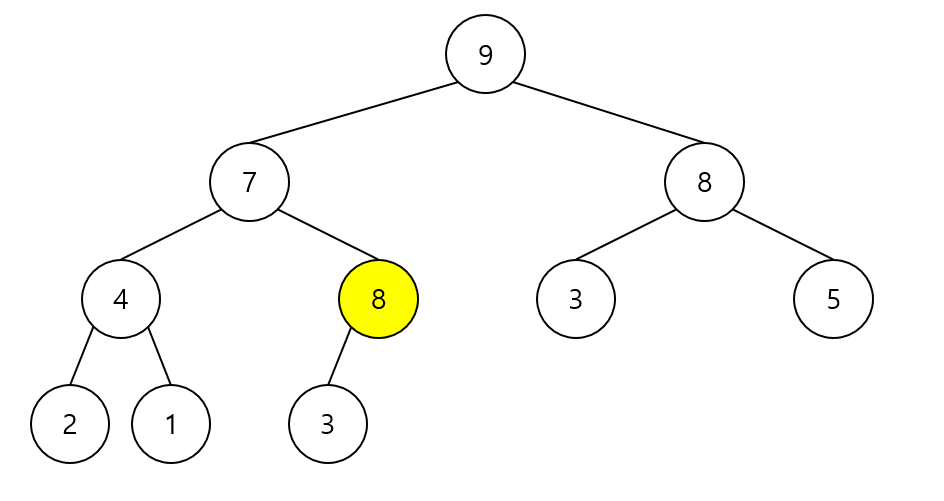
- 다시 자신의 부모 7과 비교 → 8이 더 크므로 자리 교환
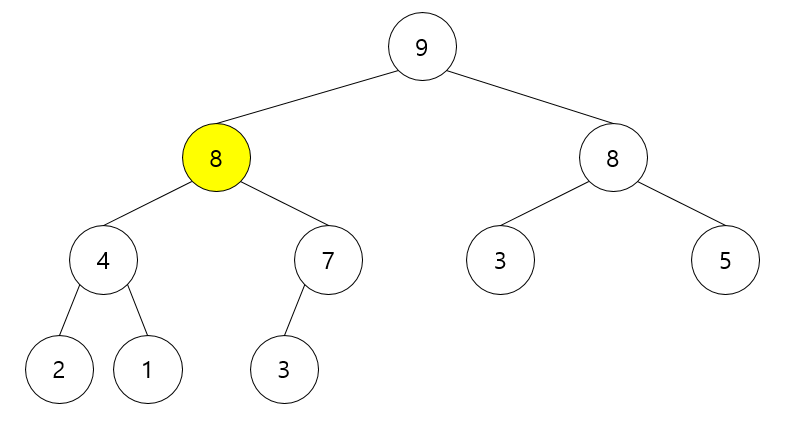
- 자신의 부모 9와 비교 → 9가 더 크므로 자리 확정
- 스며오르기(percolateUp) → 힙 성질을 충족하도록 자리를 교환하는 작업
public void insert(E newItem) {
// A[0...n-1]에 newItem을 추가
heap[numItems] = newItem;
percolateUp(numItems);
numItems++;
}
public void percolateUp(int i) {
int parentIdx = (i - 1) / 2;
if (parentIdx >= 0 && ((Comparable<E>) heap[parentIdx]).compareTo(heap[i]) < 0) {
E tmp = heap[i];
heap[i] = heap[parentIdx];
heap[parentIdx] = tmp;
percolateUp(parentIdx);
}
}삭제
힙은 우선순위 큐이므로, 가장 우선순위가 큰 (최대힙에서는 값이 제일 큰) 원소 A[0]가 삭제됨
그러나 바로 A[0]을 삭제하면 힙의 모양이 깨지기 때문에, A[n-1]와 A[0]을 바꿔준 후 A[n-1]을 삭제하고, 다시 힙의 성질을 충족할 수 있도록 원소를 교환하는 과정을 반복한다.
이 과정을 percolateDown이라고 한다.
percolateDown은 percolateUp과 유사하게, 자신의 자식 노드들 중 큰 값과 자신을 비교하며, 자식 노드가 더 클 경우 자리를 바꾸는 것이다. 이 과정은 리프 노드에 이를 때까지 계속된다.
- A[n-1]과 A[0]을 교환
- percolateDown()
public E deleteMax() {
E max = heap[0];
heap[0] = heap[this.numItems - 1]; // 자리 교환
this.numItems--; // max값은 배열에서 제외됨
percolateDown(this.numItems);
return max;
}
public void percolateDown(int i) {
int child = 2 * i + 1;
int rightChild = 2 * i + 2;
if (child <= this.numItems - 1) {
if (((Comparable<E>) heap[child]).compareTo(heap[rightChild]) < 0)
child = rightChild; // 더 큰 값을 child로 지정
if (((Comparable<E>) heap[i]).compareTo(heap[child]) < 0) {
E tmp = heap[i];
heap[i] = heap[child];
heap[child] = tmp;
percolateDown(child);
}
}
}힙 생성
리프노드가 아닌 노드부터 루트노드까지 힙 조건을 만족하도록 수정함(percolateDown)
최초의 리프노드가 아닌 노드: 맨 마지막 노드의 부모 노드 → 마지막 index가 k라면 (k-1)/2
public void buildHeap() {
if (this.numItems >= 2) {
for (int i = (numItems - 2) / 2; i >= 0; i--)
percolateDown(i);
}
}힙 수행시간
buildHeap(): Θ(n)
insert(): O(log n) - 한 번의 percolateUp (트리의 높이)
deleteMax(): O(log n) - 한 번의 percolateDown
'CS > Data Structure' 카테고리의 다른 글
| [자료구조] 트리 & 이진 탐색 트리 Binary Search Tree (자바/Java) (0) | 2022.08.16 |
|---|---|
| [자료구조] 스택 Stack & 큐 Queue (0) | 2022.08.16 |
| [자료구조] 스택 Stack 활용: 후위 표기식 계산기 (자바/Java) (0) | 2022.08.16 |
| [자료구조] B-Tree (0) | 2022.08.02 |
| [자료구조] Array, ArrayList, LinkedList (0) | 2022.07.28 |
![[자료구조] 힙 Heap](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FedCJg6%2FbtrIyw2oqeo%2FAAAAAAAAAAAAAAAAAAAAALAHhGRT56O4Z0kkxw291jxMYkEwDBd1SvBFjVcNcrsZ%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DgDS1DG7DHJlVg3p8VGaInKTNNHs%253D)